Portfolio
Naive Bayes Classifier
- When
- 2014
- Source
- Gist
- Contribution
- Solo
- Summary
A naive Bayes classifier for numeric datasets
- Sample Data Sets
This project was inspired by my Artificial Intelligence class. We had an extra credit assignment to write about the naive Bayes technique and why it was often successful and where it failed. We also needed to come up with an example to illustrate the process. After doing that, and wanting to practice Haskell, I decided to write a naive Bayes classifier in Haskell that could work with the same numeric datasets we had previously used for an assignment on Perceptrons. The program gets comparable results when run on the same datasets as the perceptron.
The following figures are demonstrations of the classifier for three different datasets, ionosphere, iris, and simple.
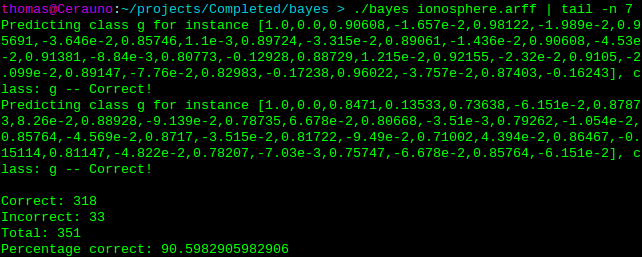
The Ionosphere dataset. The full results can be viewed on Github.
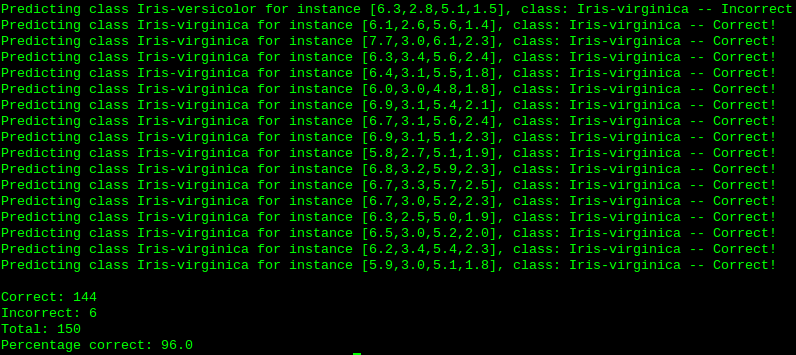
The Iris dataset. The full results can be viewed on Github.
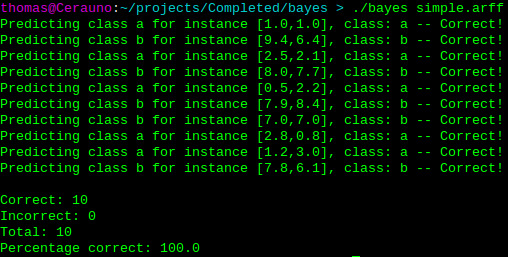
The Simple dataset. The full results can be viewed on Github.
Parallel Primes
- When
- 2013
- Source
- Github
- Contribution
- Solo
- Summary
Fast, parallel prime number sieve
- More Info
Please see the readme on Github
Can compute prime numbers up to a billion (109) in around 0.2 seconds on a Intel i7 QuadCore mobile processor. It started as an assignment for a parallel programming elective. The goal was to find all the primes up to 108 using 8 threads and splitting the work as evenly as possible. After finishing the assignment, I continued to play with it to see how far I could optimize it.
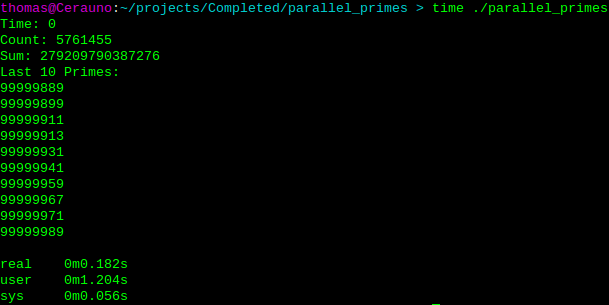
Output of the prime sieve for primes up to 109.
The limit of a billion is due to memory constraints. Going further would require working with discrete chunks and paging results to a file (a possible future project =). As it stands, it uses a number of optimizations to reduce memory requirements and speed it up, including:
- Sieving
- Multiple Threads
- Wheel Factorization
- Skip Cache
- Custom Thread Safe Bitset
- Sieving Range Reduction
I used #defines to allow options to be switched or change
their values (e.g., set the number of threads). I used the
valgrind tools to evaluate the performance of my code and
tweak it. For example, I know based on cachegrind that the
multithreading style I used leads to a large number of cache misses
(another future project).
To use wheel factorization, I wrote a program that could generate a wheel as a static array. A wheel is basically an array where successive elements indicate how far to jump to get to the next prime number candidate, skipping numbers divisible by the first n primes. As the size of wheels increases exponenetially, I only included wheels up to size 7 in my source (even that took up 6000+ lines).
Output of the wheel generator for wheels of lengths 1, 2, 3, and 4.
A noteworthy bit of code is my bitset() function. Originally, I
used a boolean byte array to keep track of which numbers were prime. This
was easy since each thread could simply write a '1' to the array to
indicate that a value was not prime. All reading was done at the end after
each thread had joined, avoiding synchronization problems. When I switched
to using a bitset (each bit is a boolean, rather than each byte), I
found I could not longer do this since to set a bit requires a read and
then a write. I solved this using GCC's
__sync_bool_compare_and_swap() function. The full code for
bitset() can be viewed in this
gist.
1
2
3
4
5
6
7
8
9
10
11
void bitset(unsigned char * array, int index){
int newval;
int oldval;
int bitset_index = index / BITS_PER_INDEX;
int bit_index = index % BITS_PER_INDEX;
do{
oldval = array[bitset_index];
newval = oldval | (1 << (bit_index));
}while(!__sync_bool_compare_and_swap(&array[bitset_index], oldval, newval));
}
source for bitset
Pong
- When
- 2012
- Source
- Github
- Contribution
- Solo
- Summary
A Pong clone written in Python. It was written using the pygame library.
The gameplay is as you would expect for the most part. The ball gains speed over time, and can be imparted with a fraction of the paddle's speed giving the player incentive to have the paddle moving when the ball hits it.

A recording of gameplay.
The blue text is debug information (paddle speed and game FPS).
Android Lockscreen Permutation Visualizer
- When
- 2013
- Source
- Github
- Contribution
- Worked with Sevena Skeels
- Summary
An android lockscreen permutation generator and visualizer.
Shows all possible Android lockscreen permutations (if given enough time...). It iteratively deepens, showing all passwords of length 4, then length 5, etc. It encodes which nodes a given node can connect to as an adjacency list. The drawing is all done in canvas.
Try me!
Slower Faster
An interactive demo of the android lockscreen permutation generator!
A video of the visualizer